Mathematics Outside of the Classroom
It was only recently that I began to enjoy solving an unfinished equation (much like the joy I experience when 'fixing' an unsolved Rubik's Cube). Math was never my forte throughout high school, and I seldom thought of it during my five-year hiatus from the world of solving for x and graphing parabolas; however, I have always understood its necessity.
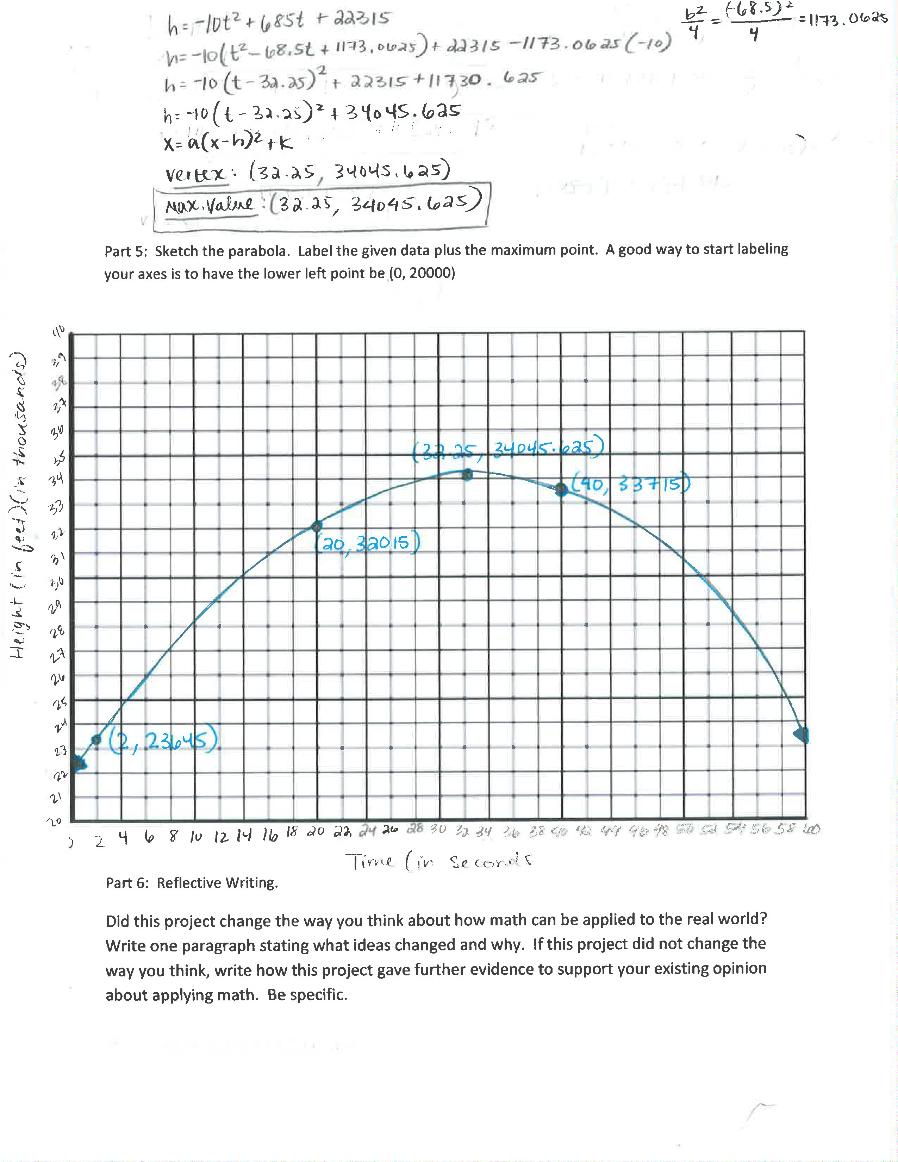
The project that I completed for Intermediate Algebra only supported the fact that math is applicable to virtually everything, whether or not one recognizes it. In essence, the laws of nature are mathematical, including the exact point in a parabolic training flight that participants experience the effects of zero gravity. Discovering this particular point, in both time and height, proved to be a bit of a challenge. I solved the system of equations using three points along the plane's path, but ran into trouble when asked to find the maximum value of the quadratic function, or the point in which zero gravity occurs. It turned out that I forgot to negate a particular number, but with my basic understanding that there is always an answer (even if that answer is 'no solution'), I knew that I was doing something wrong.
Though it may seem strange, I think the three semesters I spent immersed in the world of Philosophy has helped frame my outlook on the world of mathematics. In philosophy, a question is considered answered when it is supported by a sound, logical argument, which allows for a multitude of solutions; in math, a question is (usually) answered when the solution checks with the original equation. Though math often coincides with various philosophies (I even used it to explain the relation between free will and God's omniscience in my Philosophy of Religion paper), they are separate fields that require separate mindsets. To me, when I compare the two, math is simple because the answer is clear. It may be difficult to obtain, but I know when I find a solution, whereas philosophy has me questioning my answer repeatedly.
Overall, this class was a great experience, and when I say I looked forward to every class, I really mean it. I was incredibly uncertain of my abilities going into the semester, as I couldn't even remember slope-intercept form! But in the past few months, I have proven to myself that I cannot only do math, but I love it (so much that I regularly solved algebraic equations in my dreams--really)! I am genuinely happy that I have only touched the surface of mathematics and that I have so much more to learn. There is no part of me that thinks my continued immersion in algebra, and eventually trigonometry, calculus, and beyond, will be easy. I know that as I progress in the subject, it will only get harder and it will do so quickly; however, Intermediate Algebra has both provided me the confidence necessary to challenge myself with such topics, and, most importantly, reaffirms that my decision to major in a math-based field such as physics was in fact the right one.